This week I am focusing again on the travel cost method. The difficulty with valuing recreational sites is that they typically do not have an entrance fees, hence no recreational price. In 1949, Harold Hotelling sent a letter to the National Park Service in the US hypothesizing that the cost of travelling to a site would serve as a proxy to the price of a recreational trip (Hotelling, 1949). This hypothesis later resulted in the travel cost method.
Thus, the travel cost method (TCM) assumes that the price to recreate is the cost incurred to get to the site. This includes both fuel and time costs. The rationale behind the TCM is that the demand for recreation is inversely related to the cost to recreate. That is, there is a downward sloping demand curve for recreation. Usually, this is tested by checking whether the travel cost variable is significantly different from zero AND its coefficient has a negative sign. Most (if not all) travel cost method applications find a negative travel cost. In my previous blog posts (part 1 and part 2) I explained how to calculate the travel cost. I will skip this explanation this time.
My objective in this blog post will be to plot this recreation demand curve, and test whether the number of trips really is inversely related to the travel cost. We should get a downwards sloping demand curve for recreation, according to what the theory says.
To draw the demand curve for recreation, I use data from a recreational survey applied on Lake Eirie beaches (Sohngen et al., 2000). The objective of Sohngen et al. (2000) was to estimate the value of a single-day trip to Lake Eirie beaches. They estimated the travel cost demand function for beach visits, using counts of beach visits as the dependent variable, and the value of a beach day between $15 to $25 (depending on the beach). The data I am using can be downloaded here, under Lake Eirie Beach Data.
After estimating the demand function, Sohngen et al. (2000) find that the travel cost variable is negative and statistically different from zero across all specifications. This is as expected. The coefficient associated with travel cost can be interpreted as the expected decrease in beach trips as a response to a 1-unit increase in travel cost.
If the travel cost coefficient is negative, then plotting the demand for recreation should yield a clear relationship between travel cost and number of trips.
As usual, the first step is to import the data:
library(readxl)
lake_erie_beach_data <- read_excel("C:/DIRECTORY/lake_erie_beach_data.xls")
Firstly, I am going to look at the descriptive statistics of the variables I am interested in. trcst30 is the travel cost variable with time valued at 30% of the wage rate, while tthsbch2 is the number of beach visits (the dependent variable).
> summary(lake_erie_beach_data$trcst30) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000 9.025 18.060 24.535 36.100 135.375 2 > summary(lake_erie_beach_data$tthsbch2) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's 0.000 3.000 5.000 6.534 11.000 15.000 2
There seems to be two missing values for my variables of interest. I am going to delete these from the dataset, as well as outliers of the travel cost variable (travel cost higher than 150):
lake_erie_beach_data <- lake_erie_beach_data
[lake_erie_beach_data$trcst30<150,]
There should be a negative correlation between the two variables:
> cor(lake_erie_beach_data$trcst30[!is.na(lake_erie_beach_data$trcst30)],
lake_erie_beach_data$tthsbch2[!is.na(lake_erie_beach_data$tthsbch2)])
[1] -0.3669393
Indeed we observe a correlation of -36,69% between the two variables. This suffices to plot the two variables together already. However, the plot does not show a clean relationship:
plot(lake_erie_beach_data$trcst30[!is.na(lake_erie_beach_data$trcst30)],
lake_erie_beach_data$tthsbch2[!is.na(lake_erie_beach_data$tthsbch2)])

The graph above does not show a clear relationship unlike what I want. The problem is that the number of beach visits depends on other variables (for example income) that confound the relationship we are plotting.
Instead of plotting the number of actual trips, I can plot the predicted number of trips given other observable variables. For example, I can “clean” the variable of the number of trips from the effect of respondent’s income. The variables I will use to “clean” the number of beach visits are: male, Age, people, income, destin, pbeach, zcctcst3, zclcst3 and zgvtcst3. For an explanation on what each of these variables mean, please consult the original file.
In order to do so, I estimate an OLS model, using the lm function with all these variables but without the travel cost variable:
model <- lm(tthsbch2 ~ male + Age + people + income + destin +
pbeach + zcctcst3 + zcltcst3 + zgvtcst3,
data=lake_erie_beach_data)
summary(model)
With the estimated model I can calculate the predicted number of trips using the predict function. This yields a new vector called predictions_trips.
lake_erie_beach_data$predictions_trips <- predict(model,
data.frame(lake_erie_beach_data))
To plot two variables in R, the plot function is easy to apply. I have to identify which are the two variables. Because I have some missing values in the prediction_trips vector, I used the !is.na function below to select the subset of values that are not missing.
In the left axis I have the travel cost and in the right axis I have the number of trips.
plot(lake_erie_beach_data$predictions_trips
[!is.na(lake_erie_beach_data$predictions_trips)],
lake_erie_beach_data$trcst30
[!is.na(lake_erie_beach_data$predictions_trips)])

Althougth the graph above yields a better downwards sloping relationship between travel cost and beach visits, it is not straighforward. One problem we face when using the OLS regression to explain a count variable (like we did above) is that the predicted value of trips can be negative. This happens in the picture above: some of the predicted values for the number of trips (see along horizontal axis) are below zero.
Instead, we can use count data models, such as the Poisson or Negative Binomial. I use only the Poisson model for the sake of simplicity, by calling the command glm and specifying the family=:
model_p <- glm(tthsbch2 ~ male + Age + people + income + destin +
pbeach + zcctcst3 + zcltcst3 + zgvtcst3,
family="poisson", data=lake_erie_beach_data)
summary(model_p)
Estimate Std. Error z value Pr(>|z|)
(Intercept) 2.252e+00 2.726e-01 8.261 < 2e-16 ***
male 2.296e-01 4.603e-02 4.988 6.09e-07 ***
Age 4.152e-03 1.592e-03 2.608 0.009118 **
people -3.951e-02 9.425e-03 -4.192 2.77e-05 ***
income 1.132e-05 3.122e-06 3.625 0.000289 ***
destin 4.583e-01 6.857e-02 6.684 2.32e-11 ***
pbeach -3.474e-02 7.044e-02 -0.493 0.621858
zcctcst3 -7.996e-03 3.837e-03 -2.084 0.037193 *
zcltcst3 5.008e-03 3.419e-03 1.465 0.142945
zgvtcst3 -2.395e-02 2.579e-03 -9.285 < 2e-16 ***
Given the estimates from the Poisson model, I am once more going to predict the number of trips given these observable variables. Note that this time the command needs the type=”response” option.
lake_erie_beach_data$predictions_trips_p <- predict(model_p,
data.frame(lake_erie_beach_data),type = "response")
And now, I am going to plot the predicted number of trips from the Poisson regression with the travel cost. I am adding a few options. xlab= allows me to set a name to the x-axis, and ylab= allows me to name the y-axis. col= allows me to set a given color for the plotted data. abline is another plot which draws a trendline based on a set function. add=T adds the new plot to the old one instead of creating a new plot.
plot(lake_erie_beach_data$predictions_trips_p
[!is.na(lake_erie_beach_data$predictions_trips_p)],
lake_erie_beach_data$trcst30
[!is.na(lake_erie_beach_data$predictions_trips_p)],
xlab = "Number of Trips", ylab = "Travel Cost", col = "blue")
abline(lm(lake_erie_beach_data$trcst30
[!is.na(lake_erie_beach_data$predictions_trips_p)] ~
lake_erie_beach_data$predictions_trips_p
[!is.na(lake_erie_beach_data$predictions_trips_p)]),
add=T, col="red")
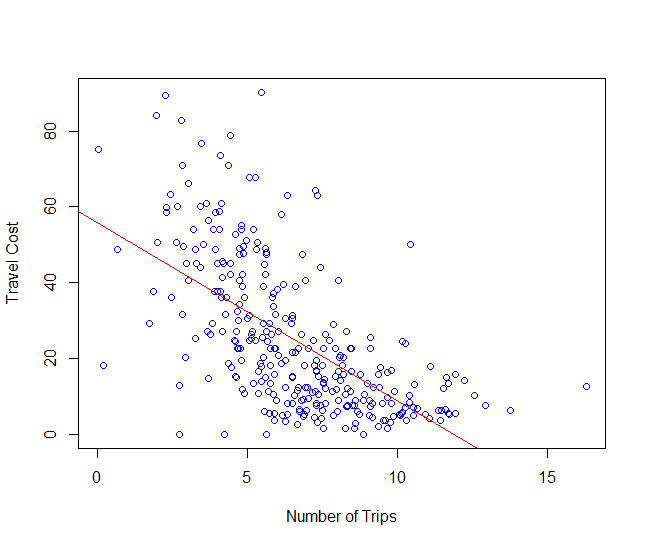
The graph above is a visual representation of the estimated demand curve for recreation. There are no negative predicted trips and the downwards sloping demand for recreation is more obvious. The blue dots are the base data and the red line is a trendline. As I expected, the demand for recreation is downwards-sloping. It confirms the travel cost method intuition that the number of trips should decrease as the travel cost increases.
References:
Hotelling, Harold. 1949. An Economic Study of the Monetary Valuation of Recreation in the National Parks. Washington, DC: U.S. Department of the Interior, National Park Service and Recreational Planning Division.
Sohngen, B., Lichtkoppler, F., & Bielen, M. (2000). The value of day trips to Lake Erie beaches. Unpublished report. Dept. of Agricultural, Environmental, and Development Economics, Ohio State University.

3 Comments